Spoiler alert: I passed my defense! 🎉
My PhD thesis is now published and available for download (Larsson 2024)! It is the culmination of five years of research on optimization other related numerical algoritms for sparse regression, in particular the lasso and sorted l-one penalized estimation (SLOPE).
In the following sections I will give an overview over the papers that are included in the thesis. This a somewhat abridged version of the paper summary section in the actual thesis and comes without a lengthy introduction to the field and these topics. If you are interested in that, I suggest you read the thesis itself!
Paper 1
The first of the papers introduces the strong screening rule for SLOPE (Larsson, Bogdan, and Wallin 2020), which is the first screening rule for SLOPE. If you haven’t heard about screening rules before, they are algorithms that discard features (predictors/variables) prior to fitting the model. They are remarkably effective for sparse methods in the high-dimensional setting and typically offer speed ups of several orders of magnitude in the high-dimensional setting. They were first discovered for the lasso with El Ghaoui, Viallon, and Rabbani (2010) and have since proven to be a key ingredient in making the lasso computationally efficient.
They are based on the following reasoning:
- The solution to a sparse regression problem is, of course, sparse, particularly in the case when the number of features (p) outnumber the number of observations (n). For the lasso, for instance, the size of the support must in fact be no larger than n.
- We can often guess quite accurately which features have little chance of being in the support, for instance by looking at the correlation between the features and the response or the solution to a problem with a larger (or smaller) penalty.1
- Even if we are wrong about which features are in the support, it is typically cheap to check if we made a mistake and refit with these features added back in.
This reasoning turns out to be pretty-much on spot and as a result screening rules have turned out to be critical for good performance for the lasso and related methods.
Screening rules are typically separated into safe and heuristic rules. Safe rules guarantee that discarded features are in fact not in the optimal solution, whereas heuristic rules do not. This division is something is something of a misnomer, however, since it is easy to check optimality conditions after fitting the model on the reduced set of features, catch any mistakes, and refit is necessary. And because safe rules sacrifice effectiveness for safety together with the fact that the optimality checks are not very expensive, it is my experience that heuristic rules typically offer better performance. They can even be used together.
The first heuristic screening rule for the lasso was introduced by Tibshirani et al. (2012): the strong screening rule. And in the first paper of my thesis, we extend this screening rule strategy to the problem of solving sorted (_1) penalized regression (SLOPE) (Bogdan et al. 2015).
I have provided some results from the first paper in Table 1. As you can see, screening improves performance considerably and offers no computational overhead even when it has little effect (as in the case of the physician data set).
| Dataset | Model | n | p | Time (No screening) | Time (Screening) |
|---|---|---|---|---|---|
| dorothea | Logistic | 800 | 88119 | 914 | 14 |
| e2006-tfidf | Least squares | 3308 | 150358 | 43353 | 4944 |
| news20 | Multinomial | 1000 | 62061 | 5485 | 517 |
| physician | Poisson | 4406 | 25 | 34 | 34 |
Paper 2
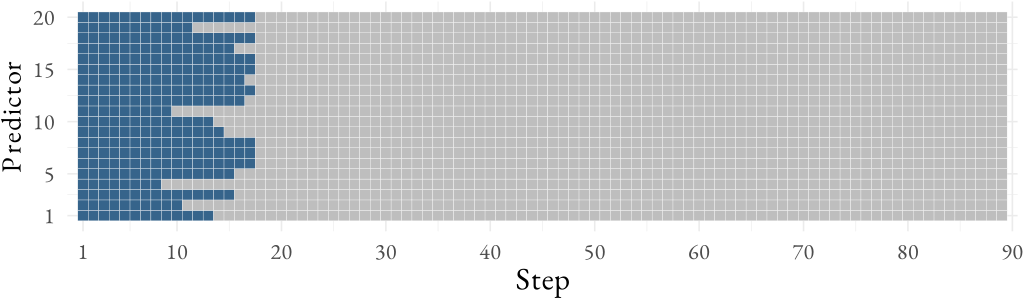
Screening rules are particularly effective when they are sequential, that is, operate along the regularization path.2 But another possibility that had previously not been explored is the idea of screening not only for the next step on the path, but for all of the remaining steps as well. This is the idea behind look-ahead screening rules, which I introduce in the second paper of the thesis, which is a short paper (Larsson 2021). We use the Gap-Safe screening rule (Ndiaye et al. 2017) here. As the name suggests, it is a safe screening rule. This means that if a feature is screened out, it is guaranteed to be zero in the solution.
As I show in the paper, the results are quite promising (Figure 2), especially since you get this kind of screening essentially for free (if you’re screening anyway).
Paper 3
Even though the strong rule for the lasso is highly effective in general, there is one area in which it struggles, namely, when features are highly correlated. Tibshirani et al. (2012) in fact noted this themselves and motivated using a modified technique: the working-set strategy (where the model is initially fit using the ever-active set, rather than the strong set) because of this.
The reason for this is that the strong rule (and every other screening rules we know of), ignores information about how close the features are to becoming active. This is the motivation for the Hessian screening rule that we introduce in the third paper of the thesis (Larsson and Wallin 2022). The name stems from the fact that we use second-order information about the optimization problem, which involves the Hessian matrix X^\intercal X. The rule offers a better estimate of the correlation vector, which in practice leads to better screening performance.
Paper 4
An ongoing problem in literature on optimization (including screening rules) is that there are now so many methods to examine and so many different models and datasets on which to compare them on, that it has become difficult to keep track of which methods it is that actually do best on a given problem. You can easily find a paper A that studies optimization methods X and Y on datasets I and II and conclude that X is better than Y but then find another paper B, which studies methods X, Y, and Z on datasets I and III and conclude that, actually, Y is better than X and, by the way, Z happens to be best of them all. Then, later, you find paper C, which claims that Z actually is considerably worse than X, which in fact also performs better for data set IV. This confused state of affairs is typically the result of authors having benchmarked their methods using different hardware, programming languages for their implementations, hyperparameters for their methods, and convergence criteria, to name a few of the many possible sources of variation.
In short, there is a dire need for a framework through which this process can be made simple, reproducible, and transparent. This is the motivation behind the benchopt package, which we present in the fourth of this thesis’ papers (Moreau et al. 2022).
The goal of benchopt is to make life easier for both researchers in optimization and users of optimization software. For a researcher who has developed a new optimization method for SLOPE, for instance, all you need to do is to write the code for your solver (optimization method) and plug it into the existing benchopt benchmark for SLOPE and run it. The package will then automatically compare your method with all the other methods in the benchmark and output table and plots of the results Figure 3. If you instead are a user who is interested in using SLOPE for your applied work and want to know which algorithm to use, you can either browse the extensive database of results that other users have already uploaded or just download the benchmark and run it yourself on the data that you are interested in using it for.
Paper 5
Proximal coordinate descent is a very efficient optimization algorithm for fitting the lasso, but it cannot handle the case when the penalty term is non-separable, which is the case in SLOPE. In practice, this has reduced the applicability of SLOPE to large data, which is unfortunate given the many appealing properties of the model.
In paper 5 (Larsson et al. 2023), however, we present a way to circumvent this issue by using a hybrid of proximal coordinate and proximal gradient descent. Our main discovery is that if we fix the clusters and optimize over each cluster in turn, rather than each feature, the problem becomes separable, which means that coordinate descent can be used. And if we combine this with proximal gradient descent steps, which allow us to discover the clusters, then we can guarantee convergence and at the same time benefit from the efficiency of coordinate descent.
The solver is illustrated for a two-dimensional SLOPE problem in Figure 4. The orange cross marks the optimum. Dashed lines indicate PGD steps and solid lines CD steps. Each dot marks a complete epoch, which may correspond to only a single coefficient update for the CD and hybrid solvers if the coefficients flip order. The CD algorithm converges quickly but is stuck after the third epoch. The hybrid and PGD algorithms, meanwhile, reach convergence after 67 and 156 epochs respectively.
Paper 6
The final paper of the thesis is a working paper in which we tackle the issue of normalization of binary features. Normalization is necessary in order to put the features on the same scale when dealing with regularized methods. What “same scale” means, however, however, is not clear, yet has been met mostly with neglect in the literature. We think that this is both surprising and problematic given the almost universal use of normalization in regularized methods and the apparent and large effects it has on the solution paths.
In our paper, we begin to bridge this knowledge gap by studying normalization for the lasso and ridge regression when they are used on binary features (features that only contain values 0 or 1) or mix of binary and normally distributed features. What we find is that there is a large effect of normalization with respect to the class balance of the features: the proportion of ones to zeros (or vice versa). Both the lasso and the ridge estimators turn out to be sensitive to this class balance and, depending on the type of normalization used, have trouble recovering effects that are associated with binary features as long as their class balance is severe enough Figure 4.
I will offer more details on this paper once work on it has been completed, but I think the results are interesting and that this field is ripe for further exploration.
References
Footnotes
This is typically the case when we are fitting a regularization path. We start with a penalty that’s large enough to make every coefficient zero and then progressively increase it.↩︎
The regularization path starts at the point where all of the model’s coefficients are zero and proceed until they are almost not penalized at all.↩︎